Большой додекаэдр

Большой додекаэдр
Тип	тело Кеплера — Пуансо
Звёздчатая форма	Правильного додекаэдра
Элементы	F = 12, E = 30, V = 12
Характеристика Эйлера	$\chi$= −6
Рёбер по граням	12{5}
Символ Шлефли	{5,5/2}
Символ Витхоффа	5/2 | 2 5
Диаграмма Коксетера
Группа симметрии	Ih, H3, [5,3], (*532)
Обозначения	U35,C44, W21
Свойства	правильный невыпуклый
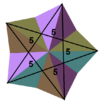(55)/2 (Вершинная фигура)	Малый звёздчатый додекаэдр двойственный многогранник

Большой додекаэдр — это тело Кеплера — Пуансо с символом Шлефли {5,5/2} и диаграммой Коксетера — Дынкина . Это один из четырёх невыпуклых правильных многогранников. Он состоит из 12 пятиугольных граней (шесть пар параллельных пятиугольников), с пятью пятиугольниками в каждой вершине, пересекающих друг друга и создающих рисунок пентаграммы.

Изображения

Прозрачная модель	Сферическая мозаика
(С анимацией)	Этот многогранник представляет сферическую мозаику с плотностью 3. (Один сферический пятиугольник выделен жёлтым цветом)
Развёртка	Звёздчатая форма
× 20 Развёртка поверхности — двадцать равнобедренных треугольных пирамид, расположенных как грани икосаэдра	Он также может быть построен как вторая (из трёх) звёздчатых форм додекаэдра и в списке Веннинджера многогранник имеет номер [W21].

Связанные многогранники

Многогранник имеет то же самое расположение рёбер, что и выпуклый правильный икосаэдр.

Если большой додекаэдр рассматривать как многогранник, имеющий нормальные треугольные грани (обычно гранью большого додекаэдра считается плоский пятиугольник, часть которого находится внутри), то он имеет ту же топологию, что и триакисикосаэдр (поверхность рода 4), но с вогнутыми пирамидами, а не выпуклыми.

Процесс усечения, применённый к большому додекаэдру даёт серию невыпуклых однородных многогранников. Усечение рёбер до их полного уничтожения (превращения в точку) даёт додекододекаэдр. Применение процесса полного усечения граней (до превращения в точку) даёт малый звёздчатый додекаэдр.

Название	Малый звёздчатый додекаэдр	Додекододекаэдр	Усечённый большой додекаэдр	Большой додекаэдр
Диаграмма Коксетера — Дынкина
Рисунок

Использование

• Этот многогранник был прообразом подобной кубику Рубика головоломки Звезда Александера.

См. также

• Соединение малого звёздчатого додекаэдра и большого додекаэдра

Литература

• М. Веннинджер. Модели многогранников. — Мир, 1974.
• Л. А. Люстерник. Выпуклые фигуры и многогранники. — М.: ГИТТЛ, 1956.
• Александров П.С., Маркушевич А.И., Хинчин А.Я. Энциклопедия элементарной математики. — ГИФМЛ, 1963. — Т. IV.

Ссылки

• Eric W. Weisstein Great dodecahedron (Uniform polyhedron) на MathWorld
• Weisstein, Eric W. Three dodecahedron stellations (англ.) на сайте Wolfram MathWorld.
• Uniform polyhedra and duals