Википедия

Круговой граф

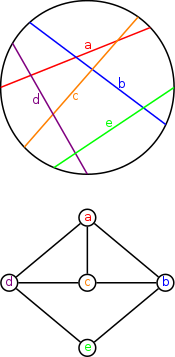
В теории графов круговой граф — это граф пересечений множества хорд окружности. То есть это неориентированный граф, вершины которого можно отождествить с хордами окружности, и эти вершины смежны тогда и только тогда, когда соответствующие хорды пересекаются.

Окружность с пятью хордами и соответствующий круговой граф.

Алгоритмическая сложность править

Спинрад[1] представил алгоритм, работающий за время O(n2), который проверяет, является ли заданный неориентированный граф с n вершинами круговым, и если он круговой, строит множество хорд, которые дают круговой граф.

Много других задач, которые NP-полны на графах общего вида, имеют алгоритмы полиномиального времени, если ограничиться круговыми графами. Например, Клокс[2] показал, что древесная ширина кругового графа может быть определена, а оптимальное дерево декомпозиции построено за время O(n3). Кроме того, наименьшее замещение (то есть хордальный граф с как можно меньшим числом рёбер, содержащий данный круговой граф в качестве подграфа) может быть найдено за время O(n3)[3]. Тискин[4] показал, что наибольшая клика кругового графа может быть найдена за время O(n log2 n), а Нэш и Грегг[5] показали, что наибольшее независимое множество невзвешенного кругового графа может быть найдено за время O(n min{d, α}), где d — параметр графа, известный как плотность, а α — число независимости кругового графа.

Всё же есть задачи, которые остаются NP-полными, даже если ограничиться круговыми графами. В эти задачи входят поиски доминирующего множества, наименьшего связного доминирующего множества и наименьшего тотального доминирующего множества[6].

Хроматическое число править

 
Хорды, образующие граф Агеева, свободный от треугольников круговой граф с 220 вершинами и хроматическим числом 5[7], представленный в виде конфигурации прямых на гиперболической плоскости.

Хроматическое число кругового графа равно наименьшему числу цветов, которые можно использовать для раскраски хорд, так, чтобы никакие две пересекающиеся хорды не имели одинакового цвета. Поскольку можно образовать круговой граф, в котором произвольное большое множество хорд пересекают друг друга, хроматическое число кругового графа может быть произвольно большим, а определение хроматического числа кругового графа является NP-полной задачей[8]. NP-полной задачей является и проверка, можно ли раскрасить круговой граф четырьмя цветами[9]. Унгер[10] утверждал, что поиск раскраски тремя цветами может быть осуществлен за полиномиальное время, но в описании его результатов отсутствуют многие детали[10].

Некоторые авторы исследовали задачи раскраски ограниченных подклассов круговых графов малым числом цветов. В частности, круговые графы, в которых нет множеств из k и более хорд, в которых все хорды пересекают друг друга, можно раскрасить, не превышая   цветов[11]. В частности, при k = 3 (то есть для круговых графов без треугольников) хроматическое число не превышает пяти, и эта граница точна — все круговые графы без треугольников могут быть выкрашены в пять цветов и существуют круговые графы без треугольников, требующие пяти цветов для раскраски[12]. Если круговой граф имеет обхват по меньшей мере пять (то есть в нём нет треугольников и циклов с четырьмя вершинами), его можно раскрасить, уложившись в три цвета[13]. Задача раскраски рамочных графов без треугольников эквивалентна задаче представления рамочных графов в виде графа, изометричного прямому произведению деревьев. В этом соответствии задач число цветов в раскраске соответствует числу деревьев в произведении[14].

Приложения править

Круговые графы появляются при проектировании СБИС как абстракция специального случая трассировки печатных плат, известного как «двуполюсная трассировка пересечений каналов». В этом случае область трассировки является прямоугольником, все сети являются двуполюсниками, а выводы располагаются по периметру прямоугольника. Легко видеть, что граф пересечений этой сети является круговым графом[15]. Одна из целей трассировки — обеспечение отсутствия электрического контакта между различными сетями и возможные пересекающиеся части должны лежать на различных слоях. Таким образом, круговые графы захватывают часть задач трассировки.

Раскраску круговых графов можно использовать также для поиска книжного вложения произвольных графов — если вершины заданного графа G расположены на окружности, а рёбра графа G образуют хорды окружности, то граф пересечений этих хорд является круговым графом, а раскраска этого кругового графа эквивалентна книжному вложению, сохраняющему круговое расположение. В этой эквивалентности число цветов соответствует числу страниц в книжном вложении[9].

Связанные классы графов править

Граф пересечений множества интервалов на прямой называется интервальным графом.

Граф является круговым тогда и только тогда, когда он является правильным интервальным графом. Это графы, вершины которых соответствуют (открытым) отрезкам на прямой и две вершины соединены ребром, если два интервала имеют непустое пересечение. При этом никакой интервал не содержится полностью в другом интервале.

Струнные графы, графы пересечений кривых на плоскости, включают круговые графы как частный случай.

Любой дистанционно-наследуемый граф является круговым графом, как и любой граф перестановки или индифферентный граф. Любой внешнепланарный граф также является круговым[16][9].

Примечания править

  1. ↑ Spinrad, 1994.
  2. ↑ Kloks, 1996.
  3. ↑ Kloks, Kratsch, Wong, 1998.
  4. ↑ Tiskin, 2010.
  5. ↑ Nash, Gregg, 2010.
  6. ↑ Keil, 1993.
  7. ↑ Ageev, 1996.
  8. ↑ Garey, Johnson, Miller, Papadimitriou, 1980.
  9. ↑ 1 2 3 Unger, 1988.
  10. ↑ 1 2 Unger, 1992.
  11. ↑ Černý, 2007. Для более ранних границ см. Gyárfás, 1985, Косточка, 1988 и Kostochka, Kratochvíl, 1997.
  12. ↑ См. Косточка, 1988 для верхней границы и Ageev, 1996 графов, достигающих нижнюю границу. Карапетян (Карапетян 1984) и (Gyárfás, Lehel 1985) указали ранее более слабые границы для той же задачи.
  13. ↑ Ageev, 1999.
  14. ↑ Bandelt, Chepoi, Eppstein, 2010.
  15. ↑ Sherwani, 2000.
  16. ↑ Wessel, Pöschel, 1985.

Литература править

  • A. A. Ageev. A triangle-free circle graph with chromatic number 5 // Discrete Mathematics. — 1996. — Т. 152, вып. 1-3. — С. 295–298. — doi:10.1016/0012-365X(95)00349-2.
  • A. A. Ageev. Every circle graph of girth at least 5 is 3-colourable // Discrete Mathematics. — 1999. — Т. 195, вып. 1-3. — С. 229–233. — doi:10.1016/S0012-365X(98)00192-7.
  • H.-J. Bandelt, V. Chepoi, D. Eppstein. Combinatorics and geometry of finite and infinite squaregraphs // SIAM Journal on Discrete Mathematics. — 2010. — Т. 24, вып. 4. — С. 1399–1440. — doi:10.1137/090760301. — arXiv:0905.4537.
  • Jakub Černý. Coloring circle graphs // Electronic Notes in Discrete Mathematics. — 2007. — Т. 29. — С. 357–361. — doi:10.1016/j.endm.2007.07.072.
  • M. R. Garey, D. S. Johnson, G. L. Miller, C. Papadimitriou. The complexity of coloring circular arcs and chords // SIAM. J. on Algebraic and Discrete Methods. — 1980. — Т. 1, вып. 2. — С. 216–227. — doi:10.1137/0601025.
  • A. Gyárfás. On the chromatic number of multiple interval graphs and overlap graphs // Discrete Mathematics. — 1985. — Т. 55, вып. 2. — С. 161–166. — doi:10.1016/0012-365X(85)90044-5.. Как процитировано у Агеева (Ageev 1996)
  • A. Gyárfás, J. Lehel. Covering and coloring problems for relatives of intervals // Discrete Mathematics. — 1985. — Т. 55, вып. 2. — С. 167–180. — doi:10.1016/0012-365X(85)90045-7.. Как процитировано у Агеева (Ageev 1996)
  • И. А. Карапетян. О совершенных дуговых и хордовых графах. — Новосибирск: Институт математики, 1984. — (Автореферат диссертации канд. Физ-матю наук: 01.01.09).
  • J. Mark Keil. The complexity of domination problems in circle graphs // Discrete Applied Mathematics. — 1993. — Т. 42, вып. 1. — С. 51–63. — doi:10.1016/0166-218X(93)90178-Q.
  • Ton Kloks. Treewidth of Circle Graphs // Int. J. Found. Comput. Sci.. — 1996. — Т. 7, вып. 2. — С. 111–120. — doi:10.1142/S0129054196000099.
  • T. Kloks, D. Kratsch, C. K. Wong. Minimum fill-in on circle and circular-arc graphs // Journal of Algorithms. — 1998. — Т. 28, вып. 2. — С. 272–289. — doi:10.1006/jagm.1998.0936.
  • А. В. Косточка. Модели и методы оптимизации / В. Т. Дементьев. — 1988. — Т. 10. — С. 204–226. — (Труды Института математики). — ISBN 5-02-028584-6, ББК В1я54 + В18я54.
  • A.V. Kostochka, J. Kratochvíl. Covering and coloring polygon-circle graphs // Discrete Mathematics. — 1997. — Т. 163, вып. 1–3. — С. 299–305. — doi:10.1016/S0012-365X(96)00344-5.
  • Nicholas Nash, David Gregg. An output sensitive algorithm for computing a maximum independent set of a circle graph // Information Processing Letters. — 2010. — Т. 116, вып. 16. — С. 630–634. — doi:10.1016/j.ipl.2010.05.016.
  • Jeremy Spinrad. Recognition of circle graphs // Journal of Algorithms. — 1994. — Т. 16, вып. 2. — С. 264–282. — doi:10.1006/jagm.1994.1012.
  • Alexander Tiskin. Proceedings of ACM-SIAM SODA 2010. — 2010. — С. 1287–1296.
  • Walter Unger. STACS 88: 5th Annual Symposium on Theoretical Aspects of Computer Science, Bordeaux, France, February 11–13, 1988, Proceedings. — Berlin: Springer, 1988. — Т. 294. — С. 61–72. — (Lecture Notes in Computer Science). — doi:10.1007/BFb0035832.
  • Walter Unger. STACS 92: 9th Annual Symposium on Theoretical Aspects of Computer Science, Cachan, France, February 13–15, 1992, Proceedings. — Berlin: Springer, 1992. — Т. 577. — С. 389–400. — (Lecture Notes in Computer Science). — doi:10.1007/3-540-55210-3_199.
  • W. Wessel, R. Pöschel. Graphs, Hypergraphs and Applications: Proceedings of the Conference on Graph Theory Held in Eyba, October 1st to 5th, 1984. — B.G. Teubner, 1985. — Т. 73. — С. 207–210. — (Teubner-Texte zur Mathematik).. Как процитировано у Unger, 1988.
  • Naveed Sherwani. Algorithms for VLSI Physical Design Automation. — Boston/Dordrecht/London: Kluwer Academic Publishers, 2000. — ISBN 0-7923-8393-1.

Ссылки править

Источник — https://ru.wikipedia.org/w/index.php?title=Круговой_граф&oldid=111432569