Симметризация Штайнера

Симметризация Штайнера — построение определённого типа, сопоставляющее произвольной фигуре фигуру с зеркальной симметрией. Это построение применяется при решении изопериметрической задачи, предложенном Якобом Штайнером в 1838.

На основе симметризации Штайнера были построены и другие симметризации, которые используются в схожих задачах.

Определение править

Пусть $H\subset \mathbb {R} ^{n}$ есть гиперплоскость и $\Phi$ — данная фигура в $\mathbb {R} ^{n}$ .

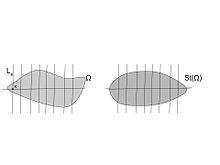
Введём ортогональную систему координат, в которой $H$ описывается уравнением $x_{n}=0$ . Для каждой точки $x\in H$ пусть $\ell _{x}$ обозначает длину пересечения перпендикуляра, проведённого к $H$ через $x$ , с множеством $\Phi$ . Далее проведём через $x$ отрезок длины $\ell _{x}$ с серединой в $x$ , перпендикулярный к $H$ . Объединение $\Phi ^{*}$ таких отрезков есть симметризация Штайнера $\Phi$ относительно $H$ .

Свойства править

Случай равенства периметров в симметризации Штайнера

Объём $\Phi ^{*}$ совпадает с объёмом $\Phi$ .

Площадь поверхности $\Phi ^{*}$ не превосходит площади поверхности $\Phi$ .
- Если $\Phi$ выпуклое тело, то равенство площадей поверхностей $\Phi ^{*}$ и $\Phi$ достигается только в случае, если $\Phi$ зеркально симметрична относительно гиперплоскости, параллельной плоскости симметризации.
- В общем случае равенство может достигаться не только для зеркально симметричных $\Phi$ , например, равенство достигается для плоских фигур, составленных из двух прямоугольников с основаниями, параллельными прямой симметризации.

Если $\Phi$ выпукла, то же верно и для $\Phi ^{*}$ .

Симметризация Штайнера не увеличивает расстояние по Хаусдорфу между фигурами, то есть
$d_{H}(\Phi ,\Psi )\geq d_{H}(\Phi ^{*},\Psi ^{*}),$

где

\Phi

и

\Psi

— произвольные фигуры,

\Phi ^{*}

и

\Psi ^{*}

— их симметризации относительно одной и той же гиперплоскости, а

d_{H}

— метрика Хаусдорфа.

Если $\Phi \subset \Psi$ , то $\Phi ^{*}\subset \Psi ^{*}$ .

Вариации и обобщения править

Круговая симметризация

Симметризация Пойа (круговая).
Осевая симметризация — аналогична симметризации Штайнера, но даёт фигуру, инвариантную относительно поворотов вокруг данной прямой.

Литература править

Бляшке. Круг и шар. — М.: Наука, 1967.