Гиперкубические соты
 Правильная квадратная мозаика. 1 color |
 Кубические соты* в их регулярной форме. 1 color |
 Шахматная квадратная мозаика 2 цвета |
 Шахматные кубические соты*. 2 цвета |
 Растянутая квадратная мозаика 3 цвета |
 Растянутые кубические соты 4 цвета |
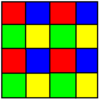 4 цвета |
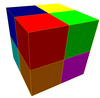 8 цветов |
Гиперкуби́ческие соты — семейство правильных сот (замощений) в пространстве размерности с символами Шлефли , имеющих симметрию группы Коксетера (или ) для .
Соты строятся из четырёх -мерных гиперкубов на каждой -мерной грани. Вершинной фигурой является гипероктаэдр .
Гиперкубические соты являются самодвойственными.
Коксетер, Гарольд назвал это семейство (для -мерных сот).
Классы построения Витхоффа по размерности править
Имеется два основных вида гиперкубических сот, правильная форма с идентичными фасетами гиперкубов и полуправильная с чередующимися фасетами, наподобие шахматной доски.
Третья форма образуется путём операции растяжения, применённой к правильной форме. В результате растяжения создаются фасеты на месте всех элементов меньшей размерности. Например, растянутые кубические соты имеют кубические ячейки с центрами исходных кубов, на исходных фасетах, на исходных рёбрах и на исходных вершинах, создавая тем самым ячейки 4-х цветов вокруг каждой вершины с соотношением 1:3:3:1.
Прямоугольные соты — это семейство топологически эквивалентных кубическим сот, но имеющих меньшую степень симметрии. В этих сотах каждое из трёх направлений может иметь отличную от других длину. Фасеты являются гиперпрямоугольниками (на плоскости это прямоугольники, а в трёхмерном пространстве — прямоугольные параллелепипеды).
| δn | Название | Символы Шлефли | Диаграммы Коксетера — Дынкина | |||
|---|---|---|---|---|---|---|
| Прямоугольные {∞}n (2m цветов, m<n) |
Правильные (Растянутые) {4,3n-1,4} (1 цвет, n цветов) |
Шахматные {4,3n-4,31,1} (2 цвета) | ||||
| δ2 | Апейрогон | {∞} | ||||
| δ3 | Квадратная мозаика | {∞}2 {4,4} |
|
|||
| δ4 | Кубические соты* | {∞}3 {4,3,4} {4,31,1} |
|
|||
| δ5 | Кубические 4-мерные соты | {∞}4 {4,32,4} {4,3,31,1} |
|
|||
| δ6 | Кубические 5-мерные соты | {∞}5 {4,33,4} {4,32,31,1} |
|
|||
| δ7 | Кубические 6-мерные соты | {∞}6 {4,34,4} {4,33,31,1} |
|
|||
| δ8 | Кубические 7-мерные соты | {∞}7 {4,35,4} {4,34,31,1} |
|
|||
| δ9 | Кубические 8-мерные соты | {∞}8 {4,36,4} {4,35,31,1} |
|
|||
| δn | Кубические n-мерные соты | {∞}n {4,3n-3,4} {4,3n-4,31,1} |
... | |||
См. также править
Литература править
- H.S.M. Coxeter. Regular Polytopes. — 3rd. — Dover edition, 1973. — ISBN 0-486-61480-8.
- стр. 122–123, 1973. (Решётка гиперкубов γn образует кубические соты δn+1)
- стр. 154–156: Частично усечённые или альтернированные, представленные префиксом h: h{4,4}={4,4}; h{4,3,4}={31,1,4}, h{4,3,3,4}={3,3,4,3}
- стр. 296, Таблица II: Правильные соты, δn+1
Для улучшения этой статьи желательно:
|







