Теорема о равнобедренном треугольнике

Теорема о равнобедренном треугольнике — классическая теорема геометрии, утверждающая, что углы, противолежащие боковым сторонам равнобедренного треугольника, равны. Эта теорема появляется как предложение 5 книги 1 «Начал» Евклида.

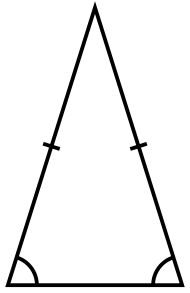
Справедливо и обратное утверждение: если два угла невырожденного треугольника равны, то стороны, противоположные им, также равны. Теорема справедлива в абсолютной геометрии, а значит и в геометрии Лобачевского, она выполняется также в сферической геометрии.

Pons asinorum править

Чертёж в доказательстве Евклида

Дьявольский мост

Эту теорему, как и (реже) Теорему Пифагора, иногда называют лат. pons asinorum^[1] — «мост ослов». Словосочетание известно с 1645 г.^[2]

Существуют два возможных объяснения такого названия. Одно состоит в том, что чертёж, используемый в доказательстве Евклида напоминал мост. Другое объяснение в том, что это первое серьёзное доказательство в «Началах» Евклида — «ослы» его осилить не могут^[1].

Доказательства править

Евклида и Прокла править

Евклид доказывает дополнительно, что если боковые стороны треугольника продолжить за основание, то углы между продолжениями и основанием тоже равны. То есть, $\measuredangle CBF=\measuredangle BCG$ на чертеже к доказательству Евклида.

Прокл указывает на то, что Евклид никогда не использует это дополнительное утверждение и его доказательство можно немного упростить, проведя вспомогательные отрезки к боковым сторонам треугольника, а не к их продолжениям. Остальная часть доказательства, проходит почти без изменений. Прокл, предположил, что второй вывод может быть использован как обоснование в доказательстве последующего предложения, где Евклид не рассмотрел все случаи.

Доказательство Прокла

Доказательство опирается на предыдущее предложение в «Началах» — на то, что сегодня называют признак равенства треугольников по двум сторонам и углу между ними.

Доказательство Прокла

Пусть $\triangle ABC$ — равнобедренный треугольник с равными сторонами $AB$ и $AC$ . Отметим произвольную точку $D$ на стороне $AB$ и построим точку $E$ на стороне $AC$ так, что $AD=AE$ . Проведём отрезки $DC$ , $BE$ и $DE$ . Поскольку $AD=AE$ , $AB=AC$ и угол $\angle A$ общий, по равенству двух сторон и угла между ними, $\triangle BAE\cong \triangle CAD$ , а значит равны их соответствующие стороны и углы. Отсюда угол $\measuredangle ABE=\measuredangle ACD$ и $\measuredangle AEB=\measuredangle ADC$ и $BE=CD$ . Поскольку $AB=AC$ и $AD=AE$ , вычитания из равных частей равные получаем $BD=CE$ . Применяя вновь признак равенства треугольников по двум сторонам и углу между ними, получаем, что $\triangle DBE\cong \triangle ECD$ . Отсюда $\measuredangle BDE=\measuredangle CED$ и $\measuredangle BED=\measuredangle CDE$ . Вычитания из равных частей равные получаем $\measuredangle BDC=\measuredangle CEB$ . Вновь по тому же признаку, получаем, что $\triangle BDC\cong \triangle CEB$ . Следовательно $\measuredangle B=\measuredangle C$ .■

Папп править

Прокл также приводит очень короткое доказательство, приписываемое Паппу. Оно проще и не требует дополнительных построений. В доказательстве применяется признак равенства по двум сторонам и углу между ними к треугольнику и его зеркальному отражению.

Доказательство Паппа

Пусть $\triangle ABC$ — равнобедренный треугольник с равными сторонами $AB$ и $AC$ . Применив признак равенства треугольников по двум сторонам и углу между ними, получаем $\triangle ABC\cong \triangle ACB$ . Действительно, эти треугольники имеют общий угол при вершине $A$ и равные прилежащие стороны $AB=AC$ . В частности, $\measuredangle B=\measuredangle C$ .■

Другие править

Доказательство Паппа иногда сбивает учеников тем, что нужно сравнивать треугольник «с самим собой». Поэтому, часто в учебниках даётся следующее более длинное доказательство. Оно проще чем доказательство Евклида, но использует понятие биссектрисы. В «Началах» построение биссектрисы угла приводится только в предложении 9. Поэтому порядок изложения приходится менять, чтобы избежать возможности кругового рассуждения.

Доказательство

Пусть $\triangle ABC$ — равнобедренный треугольник с равными сторонами $AB$ и $AC$ . Проведём биссектрису угла $\angle A$ . Пусть $X$ — точка пересечения биссектрисы со стороной $BC$ . Заметим, что $\triangle BAX\cong \triangle CAX$ поскольку $\measuredangle BAX=\measuredangle CAX$ , $AB=AC$ и $AX$ общая сторона. Значит $\measuredangle B=\measuredangle C$ .■

Лежандр использует подобные конструкции в своих «Éléments de géométrie», но, принимая $X$ как середину $BC$ . Доказательство аналогично, но использует признак равенства треугольников по трём сторонам.

Ссылки править

↑ ¹ ² Smith, David Eugene. History Of Mathematics : [англ.]. — Ginn And Company, 1925. — Vol. II : Special topics of elementary mathematics. — P. 284. — 725 p.

It formed at bridge across which fools could not hope to pass, and was therefore known as the pons asinorum, or bridge of fools.¹
…

1. The term is something applied to the Pythagorean Theorem.
↑ Definition of Pons Asinorum (англ.). Merriam-Webster. Дата обращения: 5 октября 2019. Архивировано 1 апреля 2019 года.

[Smith,_1925-1] ¹ ² Smith, David Eugene. History Of Mathematics : [англ.]. — Ginn And Company, 1925. — Vol. II : Special topics of elementary mathematics. — P. 284. — 725 p.

It formed at bridge across which fools could not hope to pass, and was therefore known as the pons asinorum, or bridge of fools.¹
…

1. The term is something applied to the Pythagorean Theorem.

[2] Definition of Pons Asinorum (англ.). Merriam-Webster. Дата обращения: 5 октября 2019. Архивировано 1 апреля 2019 года.

[1]

[2]