Дробно-линейная функция

Эта статья о дробно-линейной функции; о дробно-линейном преобразовании см. Дробно-линейное преобразование.

Дро́бно-лине́йная фу́нкция — это числовая функция, которая может быть представлена в виде дроби, числителем и знаменателем которой являются линейные функции.

Равнобочная гипербола — простейший пример дробно-линейной функции

Дробно-линейная функция, отображающая в общем случае $n$-мерное числовое пространство в одномерное числовое, представляет собой важный частный случай:

• при $n=1$ как в вещественном, так и комплексном пространстве — рациональной функции, отображающей в общем случае одномерное числовое пространство само в себя с помощью многочленов одной переменной произвольной степени;
• при $n=1$ в комплексном пространстве — дробно-линейного преобразования, отображающего в общем случае многомерное комплексное пространство само в себя;
• при $n=1$ в комплексном и при $n=2$ в вещественном пространстве, инвертируя относительно окружностей, — частный случай преобразования Мёбиуса.

Формальное определение

Дробно-линейная функция — это числовая функция вида

$\mathbb {U} ^{n}\to \mathbb {U} :w=L(u_{1},u_{2},\dots ,u_{n})={\frac {a_{1}u_{1}+a_{2}u_{2}+\cdots +a_{n}u_{n}+b}{c_{1}u_{1}+c_{2}u_{2}+\cdots +c_{n}u_{n}+d}},$

где $\mathbb {U}$ — комплексные ($\mathbb {Z}$) или вещественные ($\mathbb {R}$) числа, $u_{1},u_{2},\dots ,u_{n}$ — соответственно комплексные или вещественные переменные, $a_{1},a_{2},\dots ,a_{n},$ $c_{1},c_{2},\dots ,c_{n},$ $b,d$ — соответственно комплексные или вещественные коэффициенты,

$|c_{1}|+|c_{2}|+\dots +|c_{n}|+|d|>0$.

Возможно обобщение на кватернионы.

Вырожденные случаи:

• если

$|c_{1}|=|c_{2}|=\dots =|c_{n}|=0,$

то дробно-линейная функция становится целой линейной функций;

• если ранг матрицы

$\left({\begin{array}{cccc}a_{1}&a_{2}&\ldots &a_{n}&b\\c_{1}&c_{2}&\ldots &c_{n}&d\end{array}}\right)$

равен единице, то дробно-линейная функция вырождается в постоянную.

У собственно (невырожденной) дробно-линейной функции:

• $|c_{1}|+|c_{2}|+\dots +|c_{n}|>0;$
• равен двум ранг матрицы

$\left({\begin{array}{cccc}a_{1}&a_{2}&\ldots &a_{n}&b\\c_{1}&c_{2}&\ldots &c_{n}&d\end{array}}\right).$

Вещественная дробно-линейная функция

Вещественная дробно-линейная функция — это числовая функция вида

$\mathbb {R} ^{n}\to \mathbb {R} :y=L(x_{1},x_{2},\dots ,x_{n})={\frac {a_{1}x_{1}+a_{2}x_{2}+\cdots +a_{n}x_{n}+b}{c_{1}x_{1}+c_{2}x_{2}+\cdots +c_{n}x_{n}+d}},$

где $\mathbb {R}$ — вещественные числа, $x_{1},x_{2},\dots ,x_{n}$ — вещественные переменные, $a_{1},a_{2},\dots ,a_{n},$ $c_{1},c_{2},\dots ,c_{n},$ $b,d$ — вещественные коэффициенты,

$|c_{1}|+|c_{2}|+\dots +|c_{n}|+|d|>0$.

Функция одной переменной

Равнобочная гипербола как вещественная дробно-линейная функция ${\frac {2x-1}{x+2}}$ с асимптотами $x=-2/1=-2$ и $y=2/1=2$, $ad-bc=5>0$

В простейшем случае $n=1$ и действительных

$x_{1}=x,$ $a_{1}=a,$ $b,$ $c_{1}=c,$ $d$

график дробно-линейной функции

$y={\frac {ax+b}{cx+d}}$ —

равнобочная гипербола с асимптотами

$x=-d/c$

и

$y=a/c,$

параллельными осям координат.

Асимптоты гиперболы

Пусть дробно-линейная функция одного переменного

$y={\frac {ax+b}{cx+d}}$

несократима, то есть $ad-bc\neq 0$, и не сводится к целой линейной функции, то есть $c\neq 0$. Выделим целую часть дроби и вынесем за скобки коэффициент при $x$:

$y={\frac {\displaystyle {\frac {a}{c}}x+{\frac {b}{c}}}{\displaystyle x+{\frac {d}{c}}}}={\frac {\displaystyle {\frac {a}{c}}\left(x+{\frac {d}{c}}\right)+\left({\frac {b}{c}}-{\frac {ad}{c^{2}}}\right)}{\displaystyle x+{\frac {d}{c}}}}=$

$={\frac {a}{c}}-{\frac {ad-bc}{c^{2}\left(\displaystyle x+{\frac {d}{c}}\right)}}.$

Теперь ясно, что график функции ${\frac {ax+b}{cx+d}}$ получается из графика ${\frac {1}{x}}$ следующими элементарными преобразованиями:

• растяжением в $\left|{\frac {ad-bc}{c^{2}}}\right|$ раз по оси $Oy$, причём в случае $ad-bc>0$ с отражением относительно оси $Ox$;
• перенесением параллельно оси $Ox$ на $-{\frac {d}{c}}$;
• перенесением параллельно оси $Oy$ на ${\frac {a}{c}}$.

Таким образом, дробно-линейная функция одного переменного ${\frac {ax+b}{cx+d}}$ — это обыкновенная гипербола второго порядка, прямые $x=-{\frac {d}{c}}$ и $y={\frac {a}{c}}$ — асимптоты гиперболы, взаимно перпендикулярные и параллельные осям координат, а точка пересечения асимптот $\left(-{\frac {d}{c}},{\frac {a}{c}}\right),$ не принадлежащая кривой, — её центр.

Также очевидно, что дробно-линейная функция одного переменного ${\frac {ax+b}{cx+d}}$:

• «теряет смысл», то есть не имеет никакого значения, перестаёт «существовать» в точке $x=-{\frac {d}{c}}$;
• на интервалах $\left(-\infty ,-{\frac {d}{c}}\right)$ и $\left(-{\frac {d}{c}},+\infty \right)$ функция везде возрастает при $ad-bc>0$ и везде убывает при $ad-bc<0$;
• при неограниченном увеличении $|x|$ значения функции неограниченно приближаются к ${\frac {a}{c}}$, что видно также из преобразования

${\frac {ax+b}{cx+d}}={\frac {\displaystyle a+{\frac {b}{x}}}{\displaystyle c+{\frac {d}{x}}}}.$

Производная:

${\Biggl (}{\frac {a}{c}}-{\frac {ad-bc}{c^{2}\left(\displaystyle x+{\frac {d}{c}}\right)}}{\Biggr )}'={\frac {ad-bc}{c^{2}\left(\displaystyle x+{\frac {d}{c}}\right)^{2}}}.$

Неопределённый интеграл:

$\int {\Biggl (}{\frac {a}{c}}-{\frac {ad-bc}{c^{2}\left(\displaystyle x+{\frac {d}{c}}\right)}}{\Biggr )}dx={\frac {a}{c}}x-{\frac {ad-bc}{c^{2}}}\ln \left|x+{\frac {d}{c}}\right|+C.$

Каноническое уравнение гиперболы

Сначала приведём функцию

$y={\frac {a}{c}}-{\frac {ad-bc}{\displaystyle c^{2}\left(x+{\frac {d}{c}}\right)}}$

преобразованиями координат

$x'=x+{\frac {d}{c}},$ $y'=y-{\frac {a}{c}},$ $m=-{\frac {ad-bc}{c^{2}}}$

к простейшему виду

$y'={\frac {m}{x'}}$,

который называется уравнением обратной пропорциональности величин $x'$ и $y'$.

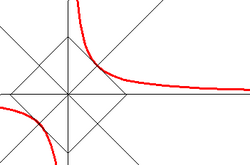
Теперь повернём координатные оси на угол $45^{\circ },$ сделав замену координат

$x'=x''\cos(45^{\circ })-y''\sin(45^{\circ })={\frac {x''-y''}{\sqrt {2}}},$

$y'=x''\sin(45^{\circ })+y''\cos(45^{\circ })={\frac {x''+y''}{\sqrt {2}}},$

получим в новых координатах:

$x'y'=m,$ ${\frac {x''-y''}{\sqrt {2}}}{\frac {x''+y''}{\sqrt {2}}}=m,$

${\frac {x''^{2}}{2m}}-{\frac {y''^{2}}{2m}}=1.$

Последнее уравнение есть каноническое уравнение равносторонней гиперболы с полуосями $a=b={\sqrt {2|m|}}.$

Функция двух переменных

Гиперболический параболоид

В случае $n=2$ и действительных $x_{1},$ $x_{2},$ $a_{1},$ $a_{2},$ $b,$ $c_{1},$ $c_{2},$ $d$ график дробно-линейной функции

$y={\frac {a_{1}x_{1}+a_{2}x_{2}+b}{c_{1}x_{1}+c_{2}x_{2}+d}}$

представляет собой гиперболический параболоид.

Комплексная дробно-линейная функция

Основная статья: Дробно-линейное преобразование

Комплексная дробно-линейная функция — числовая функция вида

$\mathbb {C} ^{n}\to \mathbb {C} :w=L(z_{1},z_{2},\dots ,z_{n})={\frac {a_{1}z_{1}+a_{2}z_{2}+\cdots +a_{n}z_{n}+b}{c_{1}z_{1}+c_{2}z_{2}+\cdots +c_{n}z_{n}+d}},$

где $\mathbb {C}$ — комплексные числа, $z_{1},z_{2},\dots ,z_{n}$ — комплексные переменные, $a_{1},a_{2},\dots ,a_{n},$ $c_{1},c_{2},\dots ,c_{n},$ $b,d$ — комплексные коэффициенты,

$|c_{1}|+|c_{2}|+\dots +|c_{n}|+|d|>0$.

Основная статья: Дробно-линейное преобразование комплексной плоскости

При $n=1$ комплексная дробно-линейная функция

$\mathbb {C} \to \mathbb {C} :w=L(z)={\frac {az+b}{cz+d}}$ —

аналитическая функция одной комплексной переменной всюду в расширенной комплексной плоскости ${\widehat {\mathbb {C} }}=\mathbb {C} \cup \{\infty \}$, за исключением точки $z=-d/c$, в которой комплексная дробно-линейная функция имеет простой полюс.

При $n\geqslant 1$ комплексная дробно-линейная функция

$\mathbb {C} ^{n}\to \mathbb {C} :w=L(z_{1},z_{2},\dots ,z_{n})={\frac {a_{1}z_{1}+a_{2}z_{2}+\cdots +a_{n}z_{n}+b}{c_{1}z_{1}+c_{2}z_{2}+\cdots +c_{n}z_{n}+d}},$ —

мероморфная функция в пространстве $\mathbb {C} ^{n}$ комплексных переменных $z_{1},z_{2},\dots ,z_{n}$, имеющая полярное множество

$\{z\in \mathbb {C} ^{n};c_{1}z_{1}+c_{2}z_{2}+\cdots +c_{n}z_{n}+d=0\}$.

Источники

• Гончаров В. Л. Элементарные функции действительного переменного. Пределы последовательностей и функций. Общее понятие функции // Энциклопедия элементарной математики. Книга третья. Функции и пределы (основы анализа) / Под ред. П. С. Александрова, А. И. Маркушевича и А. Я. Хинчина. М., Л.: Государственное издательство технико-теоретической литературы, 1952. 559 с., ил. С. 11—139.
• Долженко Е. П., Соломенцев Е. Д. Дробно-линейная функция // Математическая энциклопедия: Гл. ред. И. М. Виноградов, т. 2 Д—Коо. М.: «Советская Энциклопедия», 1979. 1104 стб., ил. Стб. 384.
• Ефимов Н. В. Краткий курс аналитической геометрии: Учебн. пособие. 13-е изд., стереот. М.: ФИЗМАТЛИТ, 2005. 238 с., ил. ISBN 5-9221-0252-4.
• Соломенцев Е. Д. Функции комплексного переменного и их применения: Учеб. пособие для студентов вузов. М.: Высш. шк., 1988. 167 с., ил. ISBN 5-06-003145-6.
• Alan F. Beardon. The geometry of discrete groups. Berlin, Heidelberg, New York: Springer-Verlag, 1983. 337 p., 93 ill.