Моде́ль Ло́тки — Вольте́рры (модель Ло́тки — Вольтерра́[1]) — модель взаимодействия двух видов типа «хищник — жертва», названная в честь своих авторов (Лотка, 1925; Вольтерра 1926), которые предложили модельные уравнения независимо друг от друга.
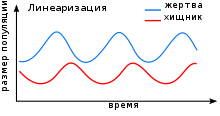
Такие уравнения можно использовать для моделирования систем «хищник — жертва», «паразит — хозяин», конкуренции и других видов взаимодействия между двумя видами[2].
В математической форме предложенная система имеет следующий вид:
- ,
- ,
где — количество жертв, — количество хищников, — время, — коэффициенты, отражающие взаимодействия между видами.
Решение системы уравнений
правитьПостановка задачи
правитьРассматривается закрытый ареал, в котором обитают два вида — травоядные («жертвы») и хищники. Предполагается, что животные не иммигрируют и не эмигрируют, и что еды для травоядных животных имеется с избытком. Тогда уравнение изменения количества жертв (без учёта хищников) принимает вид:
- ,
где — коэффициент рождаемости жертв, — величина популяции жертв, — скорость прироста популяции жертв.
Пока хищники не охотятся, они вымирают, следовательно, уравнение для численности хищников (без учёта численности жертв) принимает вид:
- ,
где — коэффициент убыли хищников, — величина популяции хищников, — скорость прироста популяции хищников.
При встречах хищников и жертв (частота которых прямо пропорциональна величине ) происходит убийство жертв с коэффициентом , сытые хищники способны к воспроизводству с коэффициентом . С учётом этого, система уравнений модели такова:
- .
Решение задачи
правитьНахождение положения равновесия системы
правитьДля положения равновесия изменение численностей популяции равно нулю. Следовательно:
- ,
- ,
из чего следует, что точка равновесия, вокруг которой происходят колебания, определяется следующим образом:
- ,
- .
Малые колебания в системе
правитьРассмотрим поведение малых отклонений численностей от их равновесных значений, то есть изменение во времени и . Из-за их малой абсолютной величины, квадратами, кубами и последующими степенями ( и ) можно пренебречь. Подставляя
- ,
- ,
в уравнения модели, получаем приближенно:
Дифференцирование одного из этих уравнений и подстановка в другое даёт следующий результат:
- ,
- .
Полученное выражение является дифференциальным уравнением гармонического осциллятора с периодом .
Конечные колебания в системе
правитьФункция
постоянна на решениях системы. Действительно:
Функция является суммой двух функций одного переменного: , где
При функция неограниченна и имеет один глобальный минимум при , в то время как при функция также неограниченна и имеет один глобальный минимум при , где и равновесные численности. Следовательно, функция имеет единственный глобальный минимум в точке , являющейся положением равновесия, а все неравновесные линии уровня при замкнуты и отвечают периодическим колебаниям с периодим, который зависит от начальных численностей.
См. также
правитьПримечания
править- ↑ П. В. Турчин. Лекция № 14. Популяционная динамика Архивная копия от 9 июня 2020 на Wayback Machine
- ↑ Одум, 1986
Ссылки
править- Популяционная динамика
- Простейшая модель «хищник-жертва»
- Николя Бакаэp, В.А. Вольперт, Д.M. Эдиев: Краткая история математической динамики населения. 2021. ISBN 979-10-343-8016-9. Pdf.
Для улучшения этой статьи желательно: |





