Аттрактор Рёсслера
Аттрактор Рёсслера — хаотический аттрактор, которым обладает система дифференциальных уравнений Рёсслера[1]:

;
где — положительные постоянные. При значениях параметров и уравнения Рёсслера обладают устойчивым предельным циклом. При этих значениях параметров в системе происходит каскад удвоения периода. При возникает хаотический аттрактор. Чётко определённые линии предельных циклов расплываются и заполняют фазовое пространство бесконечным множеством траекторий, обладающим свойствами фрактала.
Сам Рёсслер изучал систему при постоянных , и , но также часто используются и значения , , и [2].
Анализ поведения системы в плоскости
правитьДва из уравнений системы Рёсслера линейны. При они принимают вид
Поэтому устойчивость движения в плоскости определяется собственными значениями матрицы Якоби , которые равны .
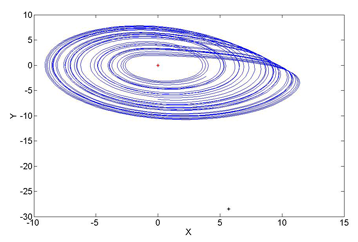
Когда , собственные значения имеют положительную вещественную часть и комплексно сопряжены. Поэтому фазовые траектории расходятся от начала координат по спирали. Теперь проанализируем изменение координаты , считая . Пока меньше , множитель в уравнении на
будет удерживать траекторию близкой к плоскости . Как только станет больше , -координата начнёт расти. В свою очередь, большой параметр начнёт тормозить рост в .
Неподвижные точки
правитьУравнения на неподвижные точки можно найти, положив производные в системе уравнений Рёсслера равными нулю. В результате оказывается, что существует две неподвижные точки:
Как видно на изображении проекции аттрактора Рёсслера выше, одна из этих точек расположена в центре спирали аттрактора, а другая находится далеко от неё.
Изменение параметров a, b и c
правитьПоведение аттрактора Рёсслера в сильно зависит от значений постоянных параметров. Изменение каждого параметра даёт определённый эффект, в результате чего в системе может возникнуть устойчивая неподвижная точка, предельный цикл или решения системы станут "убегать" на бесконечность.
Бифуркационные диаграммы являются стандартным инструментом для анализа поведения динамических систем, в том числе и аттрактора Рёсслера. Они создаются путём решения уравнений системы, где фиксируются две переменные и изменяется одна. При построении такой диаграммы получаются почти полностью «закрашенные» регионы; это и есть область динамического хаоса.
Изменение параметра a
правитьЗафиксируем , и будем изменять .
- В итоге опытным путём получим такую таблицу:
- : Сходится к устойчивой точке.
- : Крутится с периодом 2.
- : Хаос (стандартный параметр уравнений Рёсслера) .
- : Хаотичный аттрактор.
- : Аналогичен предыдущему, но хаос проявляется сильнее.
- : Аналогичен предыдущему, но хаос проявляется ещё сильнее.
Изменение параметра b
править
Зафиксируем , и будем менять теперь параметр . Как видно из рисунка, при стремящемся к нулю аттрактор неустойчив. Когда станет больше и , система уравновесится и перейдёт в стационарное состояние.
Изменение параметра c
править
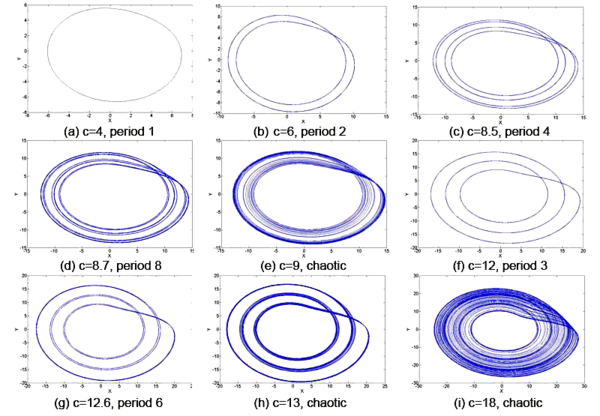
Зафиксируем и будем изменять . Из бифуркационной диаграммы видно, что при маленьких система периодична, но при увеличении быстро становится хаотичной. Рисунки показывают, как именно меняется хаотичность системы при увеличении . Например при = 4 аттрактор будет иметь период равный единице, и на диаграмме будет одна единственная линия, то же самое повторится когда = 3 и так далее; пока не станет больше 12: последнее периодичное поведение характеризуется именно этим значением, дальше повсюду идёт хаос.
Приведём иллюстрации поведения аттрактора в указанном диапазоне значений , которые иллюстрируют общее поведение таких систем — частые переходы от периодичности к динамическому хаосу.
См. также
правитьПримечания
править- ↑ Peitgen, Heinz-Otto; Jürgens, Hartmut; Saupe, Dietmar (2004), "12.3 The Rössler Attractor", Chaos and Fractals: New Frontiers of Science, Springer, pp. 636—646.
- ↑ Letellier, C.; V. Messager. Influences on Otto E. Rössler’s earliest paper on chaos (англ.) // International Journal of Bifurcation & Chaos[англ.] : journal. — 2010. — Vol. 20, no. 11. — P. 3585—3616.
Ссылки
править- Флэш-анимация
- O.E. ROSSLER — AN EQUATION FOR CONTINUOUS CHAOS (недоступная ссылка)
- Java-анимация аттракторов Рёсслера и Лоренца Архивировано 11 марта 2008 года.
- Конструктор аттракторов для MacOS
- Аттрактор Рёсслера на Scholarpedia.org
Литература
править- Воронов В. К., Подоплелов А. В. Современная физика: Учебное пособие. М., КомКнига, 2005, 512 с., ISBN 5-484-00058-0, гл. 2 Физика открытых систем. п.п 2.4 Хаотический аттрактор Рёсслера.
































