Длина окружности
Длина окружности — это длина замкнутой плоской кривой, ограничивающей круг. Поскольку окружность является границей круга или диска, длина окружности является частным случаем периметра[1][2].

Длина окружности может быть определена как предел последовательности периметров вписанных в круг правильных многоугольников при неограниченном увеличении числа сторон многоугольника[3].
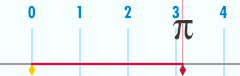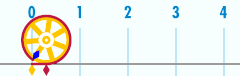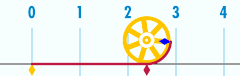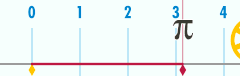

Длина окружности и число π
правитьДлина окружности связана с одной из самых важных математических констант — числом пи. Число пи обозначается греческой буквой пи ( ). Первые цифры числа в десятичной записи[4]:
определяется как отношение длины окружности к её диаметру :
Или, что эквивалентно, как отношение длины окружности к удвоенному радиусу. Формула длины окружности тогда выше принимает вид:
Использование константы является повсеместным в науке и приложениях.
В книге «Измерение круга[англ.]», написанной около 250 года до н. э., Архимед показал, что отношение ( (он не использовал обозначение ) больше 310/71, но меньше 31/7, вычислив периметры вписанного и описанного многоугольника с 96 сторонами[5]. Этот метод аппроксимации числа использовался столетиями, так как имел бо́льшую точность, чем формулы многоугольников с большим числом сторон. Последнее такое вычисление производилось в 1630 году Кристофом Гринбергером[англ.], использовавшим многоугольники с 1040 сторонами.
См. также
правитьПримечания
править- ↑ Bennett, Jeffrey; Briggs, William (2005), Using and Understanding Mathematics / A Quantitative Reasoning Approach (англ.) (3rd ed.), Addison-Wesley, p. 580, ISBN 978-0-321-22773-7
- ↑ San Diego State University. Perimeter, Area and Circumference. Addison-Wesley (2004). Дата обращения: 6 марта 2020. Архивировано из оригинала 6 октября 2014 года.
- ↑ Jacobs, Harold R. (1974), Geometry (англ.), W. H. Freeman and Co., p. 565, ISBN 0-7167-0456-0
- ↑ Sloane, N. J. A. Sequence A000796, On-Line Encyclopedia of Integer Sequences OEIS, OEIS Foundation.
{{citation}}: Википедия:Обслуживание CS1 (числовые имена: authors list) (ссылка) - ↑ Katz, Victor J. (1998), A History of Mathematics / An Introduction (англ.) (2nd ed.), Addison-Wesley Longman, p. 109, ISBN 978-0-321-01618-8
Литература
править- Атанасян Л. С., Бутузов В. Ф. и др. Дополнительные главы к учебнику 8 класса // Геометрия. — 3-е издание. — М.: Вита-Пресс, 2003.
- Выгодский М. Я. Справочник по элементарной математике. — М.: Наука, 1978.
- Переиздание: М.: АСТ, 2006, ISBN 5-17-009554-6, 509 стр.

