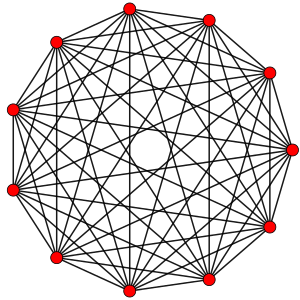
Правильный 10-симплекс
Тип
Правильный десятимерный политоп
Символ Шлефли
{3,3,3,3,3,3,3,3,3}
9-мерных ячеек
11
8-мерных ячеек
55
7-мерных ячеек
165
6-мерных ячеек
330
5-мерных ячеек
462
4-мерных ячеек
462
Ячеек
330
Граней
165
Рёбер
55
Вершин
11
Вершинная фигура
Правильный 9-симплекс
Двойственный политоп
Он же (самодвойственный )
Правильный 10-симплекс , или гендекаксеннон , или гендека-10-топ — правильный самодвойственный десятимерный политоп . Имеет 11 вершин, 55 рёбер, 165 граней - правильных треугольников, 330 правильнотетраэдрических ячеек, 462 пятиячейниковых 4-ячейки, 462 5-ячейки, имеющих форму правильного 5-симплекса , 330 6-ячеек, имеющих форму правильного 6-симплекса , 165 7-ячеек, имеющих форму правильного 7-симплекса , 55 8-ячеек, имеющих форму правильного 8-симплекса и 11 9-ячеек, имеющих форму правильного 9-симплекса . Его двугранный угол равен arccos(0,1) , то есть примерно 84,26°.
Правильный 10-сипмлекс можно разместить в Декартовой системе координат следующим образом (длина ребра тела равна 2 и центр приходится на начало координат):
(
1
/
55
,
1
/
45
,
1
/
6
,
1
/
28
,
1
/
21
,
1
/
15
,
1
/
10
,
1
/
6
,
1
/
3
,
±
1
)
{\displaystyle \left({\sqrt {1/55}},\ {\sqrt {1/45}},\ 1/6,\ {\sqrt {1/28}},\ {\sqrt {1/21}},\ {\sqrt {1/15}},\ {\sqrt {1/10}},\ {\sqrt {1/6}},\ {\sqrt {1/3}},\ \pm 1\right)}
(
1
/
55
,
1
/
45
,
1
/
6
,
1
/
28
,
1
/
21
,
1
/
15
,
1
/
10
,
1
/
6
,
−
2
1
/
3
,
0
)
{\displaystyle \left({\sqrt {1/55}},\ {\sqrt {1/45}},\ 1/6,\ {\sqrt {1/28}},\ {\sqrt {1/21}},\ {\sqrt {1/15}},\ {\sqrt {1/10}},\ {\sqrt {1/6}},\ -2{\sqrt {1/3}},\ 0\right)}
(
1
/
55
,
1
/
45
,
1
/
6
,
1
/
28
,
1
/
21
,
1
/
15
,
1
/
10
,
−
3
/
2
,
0
,
0
)
{\displaystyle \left({\sqrt {1/55}},\ {\sqrt {1/45}},\ 1/6,\ {\sqrt {1/28}},\ {\sqrt {1/21}},\ {\sqrt {1/15}},\ {\sqrt {1/10}},\ -{\sqrt {3/2}},\ 0,\ 0\right)}
(
1
/
55
,
1
/
45
,
1
/
6
,
1
/
28
,
1
/
21
,
1
/
15
,
−
2
2
/
5
,
0
,
0
,
0
)
{\displaystyle \left({\sqrt {1/55}},\ {\sqrt {1/45}},\ 1/6,\ {\sqrt {1/28}},\ {\sqrt {1/21}},\ {\sqrt {1/15}},\ -2{\sqrt {2/5}},\ 0,\ 0,\ 0\right)}
(
1
/
55
,
1
/
45
,
1
/
6
,
1
/
28
,
1
/
21
,
−
5
/
3
,
0
,
0
,
0
,
0
)
{\displaystyle \left({\sqrt {1/55}},\ {\sqrt {1/45}},\ 1/6,\ {\sqrt {1/28}},\ {\sqrt {1/21}},\ -{\sqrt {5/3}},\ 0,\ 0,\ 0,\ 0\right)}
(
1
/
55
,
1
/
45
,
1
/
6
,
1
/
28
,
−
12
/
7
,
0
,
0
,
0
,
0
,
0
)
{\displaystyle \left({\sqrt {1/55}},\ {\sqrt {1/45}},\ 1/6,\ {\sqrt {1/28}},\ -{\sqrt {12/7}},\ 0,\ 0,\ 0,\ 0,\ 0\right)}
(
1
/
55
,
1
/
45
,
1
/
6
,
−
7
/
4
,
0
,
0
,
0
,
0
,
0
,
0
)
{\displaystyle \left({\sqrt {1/55}},\ {\sqrt {1/45}},\ 1/6,\ -{\sqrt {7/4}},\ 0,\ 0,\ 0,\ 0,\ 0,\ 0\right)}
(
1
/
55
,
1
/
45
,
−
4
/
3
,
0
,
0
,
0
,
0
,
0
,
0
,
0
)
{\displaystyle \left({\sqrt {1/55}},\ {\sqrt {1/45}},\ -4/3,\ 0,\ 0,\ 0,\ 0,\ 0,\ 0,\ 0\right)}
(
1
/
55
,
−
3
1
/
5
,
0
,
0
,
0
,
0
,
0
,
0
,
0
,
0
)
{\displaystyle \left({\sqrt {1/55}},\ -3{\sqrt {1/5}},\ 0,\ 0,\ 0,\ 0,\ 0,\ 0,\ 0,\ 0\right)}
(
−
20
/
11
,
0
,
0
,
0
,
0
,
0
,
0
,
0
,
0
,
0
)
{\displaystyle \left(-{\sqrt {20/11}},\ 0,\ 0,\ 0,\ 0,\ 0,\ 0,\ 0,\ 0,\ 0\right)}