Переходный процесс

Перехо́дный проце́сс — в теории систем представляет собой изменения координат динамической системы во времени до некоторого установившегося состояния; возникает под влиянием возмущающих воздействий, изменяющих её состояние, структуру или параметры, а также вследствие ненулевых начальных условий.

Затухающие колебания — типичный переходный процесс, при котором некоторый параметр какое-то время колеблется вокруг установившегося значения

Характеристики

Изучение переходных процессов — важный шаг в процессе анализа динамических свойств и качества рассматриваемой системы. Широкое применение нашло экспериментальное и аналитическое определение и построение переходных процессов для наиболее неблагоприятных условий работы динамической системы при внешних возмущениях типа дельта-функции, ступенчатом или синусоидальных воздействиях.

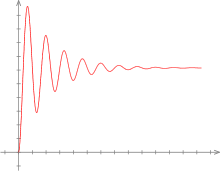
Оценка качества САУ по виду кривой переходного процесса производится при помощи так называемых прямых показателей качества — перерегулирования, допустимого числа колебаний и времени переходного процесса. Обычно рассматривают переходный процесс, возникающий в системе при воздействии единичной ступенчатой функции, т. е. переходная функция замкнутой системы.

Время переходного процесса

Длительность переходного процесса в системе характеризует её быстродействие, а его характер определяет качество системы. За количественную характеристику длительности переходного процесса принимают время, необходимое выходному сигналу системы для того, чтобы приблизиться к своему установившемуся значению, т. е. время, по истечении которого выполняется равенство:

$|h(t)-h_{st}|\leqslant \epsilon ,$

где $h_{st}$ — установившееся значение;

$\epsilon$ — наперёд заданное положительное число.

В линейных непрерывных динамических системах принято рассматривать переходной процесс, вызванный единичным ступенчатым возмущением, но в этом случае установившееся значение достигается за бесконечно большое время. Если же ограничить точность достижения установившегося значения некоторой малой величиной $\epsilon$, то тогда длительность переходного процесса $t$ будет конечной величиной.

В приложениях теории управления обычно в САУ принимают $\epsilon$ равной 0,01—0,05 от $h_{st}$, т. е. переходный процесс считают закончившимся, когда переходная функция отличается не более, чем на 1–5 % от своего установившегося (стационарного) значения.

Перерегулирование

Перерегулирование (определяется величиной первого выброса) — отношение разности максимального значения переходной характеристики и её установившегося значения к величине установившегося значения. Измеряется обычно в процентах.

Степень затухания переходного процесса

Степень затухания переходного процесса определяется относительным уменьшением соседних амплитуд переходной характеристики.

Числителем является амплитуда первого колебания. Степень затухания показывает во сколько раз уменьшается амплитуда второго колебания по сравнению с первым.

Степень затухания системы зависит от показателя колебательности $M$ (см. ниже).

Логарифмический декремент колебания

Логарифмический декремент колебания — натуральный логарифм отношения амплитуд двух соседних перерегулирований. Обратная ему величина показывает, за какое число колебаний их амплитуда уменьшается в $e$ раз ($e$ — основание натуральных логарифмов). Уместен лишь для характеристики линейных систем.

Колебательность

Характеризует склонность системы к колебаниям и определяется как модуль отношения амплитуд второго колебания к амплитудам первого колебания. Колебательность системы характеризуют при помощи показателя колебательности $M$, который представляет собой отношение резонансного пика при резонансной частоте к значению АЧХ при нулевой частоте.

Показатель колебательности связан со степенью колебательности формулой:

$M={\frac {1+m^{2}}{2m}}.$

При увеличении $M$, уменьшается показатель колебательности $m$ и соответственно происходит уменьшение степени колебательности.

Установившаяся ошибка

Установившаяся ошибка системы — разница между предполагаемым и реальным значением выходного сигнала при времени, стремящемся к бесконечности. В идеальных астатических системах установившаяся ошибка равна нулю.

Примеры

Электрические цепи

Основная статья: Переходные процессы в электрических цепях

В электрической цепи переходный процесс характеризуется плавным инерционным изменением тока и напряжения в цепи в ответ на приложенное внешнее воздействие.

Формула, описывающие протекание простейших переходных процессов (разряд конденсатора через резистор):

$U(t)=U_{0}e^{(-t/\tau )},\$ $\tau =RC,$

где $U_{0}$ — значение напряжения на конденсаторе в момент перед началом переходного процесса,

$\tau$ — постоянная времени переходного процесса, С — ёмкость, R — сопротивление элементов цепей.

Для цепей, содержащих индуктивность, если можно пренебречь активным сопротивлением, постоянная времени равна:

$\tau =L/R.$

См. также

• Бифуркационная память
• Время изодрома
• Зона нечувствительности
• Коэффициент демпфирования
• Переходные процессы в электрических цепях

Литература

Книги