Розетта Клемперера
Розетта Клемперера — гравитационная система лёгких и тяжёлых тел, обращающихся по регулярно повторяющимся орбитам вокруг общего центра масс. Она была впервые описана Вольфгангом Клемперером в 1962 году[1]. Клемперер описывал систему следующим образом: «Такая симметрия также присуща своеобразной семье геометрических конфигураций, которые можно описать как „розетты“. В них присутствует чётное число „планет“ двух (и более) типов, один (или несколько) наборов которых тяжелее других, причём все планеты, принадлежащие к одному набору (имеющие одинаковую массу), располагаются в углах двух (или более) чередующихся правильных многоугольников так, что лёгкие и тяжёлые чередуются (или следуют друг за другом циклическим образом)».
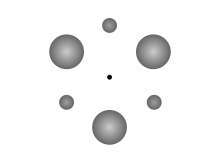
Простейшая розетта будет состоять из ряда четырёх чередующихся тяжёлых и лёгких тел, находящихся на угловом расстоянии 90 градусов друг от друга, в ромбической конфигурации [тяжёлое, лёгкое, тяжёлое, лёгкое], причём два тяжёлых тела имеют одинаковую массу, как и два лёгких тела. Число типов тел по массе может быть увеличено, пока порядок расположения остаётся циклическим: например, [1,2,3 … 1,2,3 ], [ 1,2,3,4,5 … 1,2,3,4,5 ], [ 1,2,3,3,2,1 … 1,2,3,3,2,1 ]. Клемперер упоминал о восьмиугольных и ромбических розеттах.
Неверное использование
правитьТермин «розетта Клемперера» (нередко в ошибочном написании: «розетта Кемплерера») часто используется для описания конфигурации из трёх и более равных масс, расположенных в вершинах равностороннего многоугольника, имеющих одинаковую угловую скорость относительно их центра масс. Клемперер упоминает такую конфигурацию в начале своей статьи, но только как представителя уже известного набора находящихся в равновесии систем, до описания собственно розетты.
В романе Ларри Нивена «Мир-Кольцо» «флот миров» кукольников Пирсона расположен в такой конфигурации (5 планет в вершинах пятиугольника), которую Нивен называет «розеттой Кемплерера». Это (возможно, намеренное) искажённое написание (и ошибочное использование), может являться источником подобного недоразумения. Другой возможный источник искажения написания — сходство имён Кемплерера и Иоганна Кеплера, описавшего законы движения планет в XVII веке.
Неустойчивость
правитьМоделирование этой системы[2] (или простой линейный анализ возмущений) показывает, что такая система, безусловно, неустойчива: любое отклонение от идеальной геометрической конфигурации вызывает колебания, которые в конечном итоге приводят к разрушению системы (в исходной статье Клемперер также отмечает этот факт). Результат не зависит от того, находится ли в центре розетты пустое пространство, или она обращается вокруг звезды.
Объяснение неустойчивости состоит в том, что любое тангенциальное возмущение приводит к тому, что одно из тел приближается к одному из своих соседей и отдаляется от другого, в результате чего сила притяжения к ближнему соседу становится больше, а по отношению к дальнему — меньше, в результате чего возмущённый объект начинает двигаться к ближнему соседу, что увеличивает возмущение, а не компенсирует его. Радиальное возмущение, направленное внутрь, приводит к тому, что возмущённое тело, становится ближе ко всем другим объектам, в результате чего увеличивается сила их взаимодействия и орбитальная скорость, что косвенно приводит к тангенциальному возмущению (результат которого описан выше). Таким образом, описанная Ларри Нивеном розетта Кукольников требовала бы искусственной стабилизации.
Примечания
править- ↑ Klemperer, W. B. Some Properties of Rosette Configurations of Gravitating Bodies in Homographic Equilibrium (англ.) // Astronomical Journal : journal. — 1962. — April (vol. 67, no. 3). — P. 162—167. — doi:10.1086/108686. — .
- ↑ Jenkins, Bob Klemperer Rosettes. Дата обращения: 12 января 2007. Архивировано 8 сентября 2012 года.