Число пересечений (теория узлов)

В теории узлов число пересечений узла — это наименьшее число пересечений на любой диаграмме узла. Число пересечений является инвариантом узла.

Трилистник без симметрии 3-го порядка с помеченными пересечениями

Таблица всех простых узлов с семью или меньше пересечениями (зеркальные варианты не включены)

См. также: Минимальное число пересечений рёбер графа

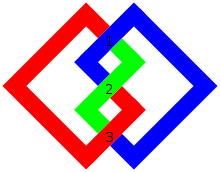
Примеры

В качестве примера: тривиальный узел имеет нулевое число пересечений, число пересечений трилистника равно трём, а число пересечений восьмёрки равно четырём. Больше нет узлов с числом пересечений четыре и меньше, и есть только два узла с числом пересечений пять, но число узлов с конкретными числами пересечений быстро растёт по мере роста числа пересечений.

Таблицы

Таблицы простых узлов традиционно индексируются числом пересечений с дополнительным описанием, какой именно узел из множества узлов с заданным числом пересечений имеется в виду (это упорядочение не базируется на каких-либо свойствах, за исключением торических узлов, для которых скрученные узлы перечисляются первыми). Список начинается с 3₁ (трилистник), 4₁ (восьмёрка), 5₁, 5₂, 6₁, и так далее. Этот порядок существенно не изменился со времён Тэта, опубликовавшего таблицу в 1877 году.

Аддитивность

Имеется очень малый прогресс в понимании поведения числа пересечений при элементарных операциях на узлах. Большой открытый вопрос — является ли число пересечений аддитивной по отношению к операции конкатенации. Также ожидается, что сателлитный узел узла K будет иметь большее число пересечений, чем K, но это не доказано.

Аддитивность числа пересечений конкатенации узлов доказана для специальных случаев, например, если исходные узлы являются альтернированными или если исходные узлы являются торическими. Марк Лакенбай дал доказательство, что существует константа N > 1, такая что ${\frac {1}{N}}(\mathrm {cr} (K_{1})+\mathrm {cr} (K_{2}))\leq \mathrm {cr} (K_{1}+K_{2})$, но его метод, использующий нормальные поверхности, не может улучшить N до 1.

Приложение в биоинформатике

Имеется странная связь между числом пересечений узла и физическим поведением узлов ДНК. Для простых узлов ДНК число пересечений является хорошим предсказателем относительной скорости узла ДНК электрофореза геля агарозы. В основном, более высокое число пересечений приводит к большей относительной скорости.

Связанные инварианты

Имеются связанные понятия среднего числа пересечений и асимптотического числа пересечений. Оба этих понятия определяют границы стандартного числа пересечений. Есть гипотеза, что асимптотическое число пересечений равно числу пересечений.

Другие числовые инварианты узла включают число мостов, коэффициент зацепления, число отрезков и число распутывания.

Литература

• Simon Jonathan. Energy functions for knots: Beginning to predict physical behavior // Mathematical Approaches to Biomolecular Structure and Dynamics / Jill P. Mesirov, Klaus Schulten, De Witt Sumners. — 1996. — Т. 82. — (The IMA Volumes in Mathematics and its Applications). — doi:10.1007/978-1-4612-4066-2_4.
• P. G. Tait. On Knots I, II, III // Scientific papers. — Cambridge University Press, 1898. — Т. 1.
• C. A. Adams. The Knot Book: An Elementary Introduction to the Mathematical Theory of Knots. — American Mathematical Society, 2004. — ISBN 9780821836781.
• H. Gruber. Estimates for the minimal crossing number. — 2003. — arXiv:math/0303273.
• Yuanan Diao. The additivity of crossing numbers // Journal of Knot Theory and its Ramifications. — 2004. — Т. 13, вып. 7. — doi:10.1142/S0218216504003524.
• Marc Lackenby. The crossing number of composite knots // Journal of Topology. — 2009. — Т. 2, вып. 4. — doi:10.1112/jtopol/jtp028.