Зоноэдр

Зоноэдр — многогранник, представимый как сумма Минковского конечного числа отрезков. Зоноэдры в $n$-мерном пространстве называются также зонотопами.

Гексоромбододекаэдр — пример зоноэдра

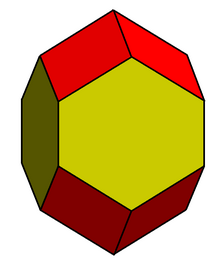
Впервые определены и исследованы Евграфом Степановичем Фёдоровым.

Двумерный многоугольный аналог зоноэдра называется зоногоном.

Свойства

• Зоноэдр — выпуклый многогранник, причём сам зоноэдр и его грани всех размерностей центрально симметричны.
• Наличия центров симметрии у всех двумерных граней выпуклого многогранника достаточно, чтобы он был зоноэдром.
• Всякий зоноэдр есть проекция гиперкуба достаточно высокой размерности.
• Всякий зоноэдр есть центральное сечение гипероктаэдра достаточно высокой размерности.
• Всякий зоноэдр равносоставлен кубу.

Вариации и обобщения

• В классе центрально симметричных выпуклых тел особую роль играют зоноиды — тела, предельные для зоноэдров. Они допускают специфическое интегральное представление опорной функции и являются конечномерными сечениями шара в банаховом пространстве L¹.

Ссылки

• «Зоопарк зоноэдров»